Let’s consider for a moment the “next” communicable virus. You show no symptoms but you try a home testing kit anyway, expecting the result to be negative. To your great surprise, the result is positive! The information enclosed in the testing kit package explained that the test results are nearly 100% accurate and incidence rates for false positives is near zero. If you are like most people, you’d be concerned about this and contact your doctor. In an effort to allay your concern, the doctor explains that even with your positive test result, there is only a 3% chance of you becoming ill. How is this possible?
In this blog, we’ll explain this phenomenon, known as the FP (false-positive) Paradox.
True positive or false concern?
Let’s have a look at the case of the peaceful and fictitious island of Panicland, situated in the middle of the ocean. Paniclanders enjoyed the relative disconnect from the outside world. Everything was calm until one day, a mysterious disease spread across the island. People began to show symptoms that were not seen before. Based on the symptoms, it seemed that the real communicable virus COVID-19 had come to Panicland. It is known that the disease is affecting one-tenth of one percent of Panicland’s population (1 in 1,000). COVID-19 test kits arrive. Authorities say the test can detect COVID-19 in 98% of patients and the false-positive rate (FPR) is 3%. FPR is the chance that a person not carrying COVID-19 tests positive.
Panicland administers tests to all its 100,000 residents. One fellow, we’ll call him Mr. Fear, tested positive for COVID-19. Mr. Fear was frightened. Was this justified?
Most people will look at the test outcome and believe it is completely reliable, given the high detection rate and very low incidence of false positives. The more important metric, however, is that most people ignore the sampling space. In other words, what is the likelihood of the phenomenon we are looking for? In this case – getting infected with COVID-19. Let’s try to demonstrate that:
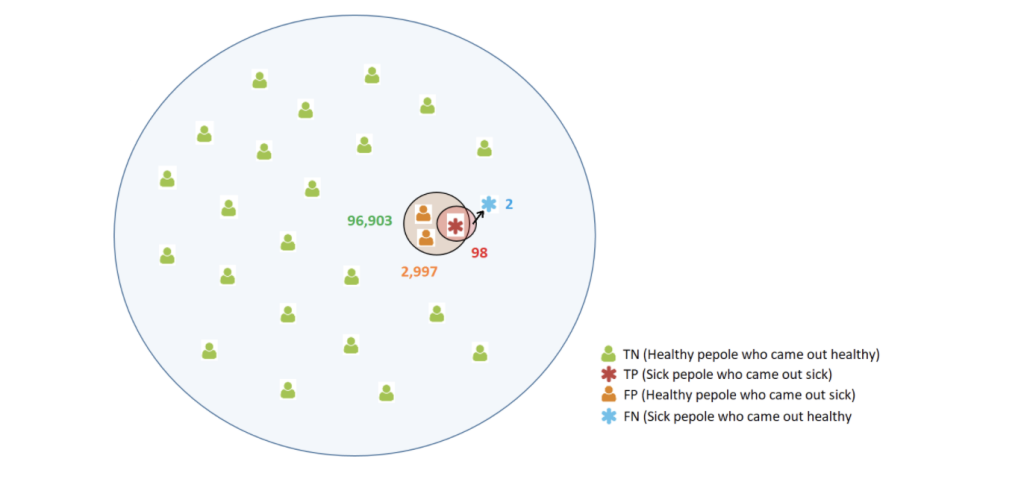
Figure 1: Diagnostic test results among 100,000 residents.
Assumptions: 1 out of 1,000 is infected, the test has an accuracy of 98% with 3% FPR.
If so, there will be 1/1000*100K = 100 sick people on the island. 98% success rate leads to 100*0.98=98 sick people who will be diagnosed as such and 2 that that will be missed. Due to 3% of FPR, we will get that among the 99,900 healthy people on the island a total of 99,900*0.03=2,997 people mistakenly identified as sick. The rest of them, 99,900*0.97=96,903 residents, will be truly classified as healthy.
What are the chances that someone who tested positive is indeed infected? Here, the sampling space or the likelihood of the phenomenon is 1/1000, meaning only 100 residents out of 100,000 will actually get infected. Note that out of 3,095 positive results (98+2,997) only 98 are true while the rest of them are FP, meaning that the chance of being truly ill is only 98/3,095=3.1%. A person with a positive test result has just a 3.1% chance of getting sick.
If we take this exercise one step further to the extreme and assume that there is only one real patient on the whole island and repeat the calculation, we will get that a positive result means a chance of only 0.03% that you are really sick!
“When a paradox is widely believed, it is no longer recognized as a paradox.” – Mason Cooley
The FP paradox
Let’s take a closer look at what happened here. How is it that systems that are considered to be reliable such as disease tests become almost useless by mistakenly predicting a large population as positive?
“By denying scientific principles, one may maintain any paradox.” – Galileo Galilei
The one thing you might notice is that the phenomena we are looking for are still rare (0.1% for our COVID-19 example). The attempt to predict rare traits in a large population using a system without high certainty will lead to a high number of false positives. This fallacy is known as the FP paradox, a private example of the base rate neglect case where people tend to ignore general information and use only specific information rather than integrating both of them. The paradox refers to the case where there are significantly more false-positive predictions than true positives.
For example, if we assume that the COVID-19 is not a negligible phenomenon and about 30% of Panicland’s inhabitants have been infected at a given time, we will get that a positive result indicates a 93% chance of actually being infected as opposed to 3.1% we had before.
When you see a doctor and describe your symptoms, they will order testing for the diseases they suspect you might have. They will not order tests unrelated to your symptoms, because of the price and not less important, the chance for FP result.
Bottom line:
If a test is uncertain, it can be problematic in detecting rare phenomena.
The main pitfall in the previous cases was that we were looking for rarer cases than the FP rate of the system we used. This was the case when we tried to detect disease with a probability of 0.1% using a system that suffered from a false-positive rate of 3%.
The FP paradox relates to cases where there are more false-positive results than true positives. A rule of thumb regarding these systems in order to avoid such cases is to demand that:
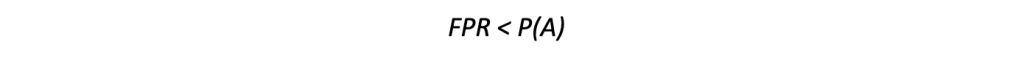
Equation 1: Avoiding the FP Paradox
where FPR is the false-positive rate of the system we used for detection and P(A) is the real probability of the phenomenon that we are trying to predict.
We will end this section by describing the paradox for one of the most reliable tests there is – a pregnancy test. The reason for the great accuracy of these tests is that it is sampled not from a random set of women, where the true chances of being pregnant will probably be small, but those who are suspected of carrying a fetus, meaning that the real probability of the phenomenon (pregnant women) is not negligible. Just imagine a case where we will perform this test on a randomly sampled population, including men and women. How many cases of false positives will there be in this experiment?
The COVID-19 self-test dilemma
Rapid home kit tests for COVID-19 are the main strategy for breaking the chain of infection. Some countries are planning to or have already given all school and kindergarten students a rapid antigen diagnostic test before the start of the school year. Examples of this can be found in Israel or in the second-largest school district of Los Angeles. As we can see, one has to be very careful when running a test with a large or equal amount of FPs to the phenomenon probability we are looking for on large populations.
Let’s take a look at some of the numbers that are relevant for the time of writing this blog (mid-August 2021). In Israel, there are currently 2.3 million students in school and kindergartens. The number of verified cases is currently 32,736. Dr. Anthony Fauci estimated that 40% of infections are asymptomatic, meaning that the actual number of infections including the unverified cases is about 55,000. That is, the probability of the phenomenon is about 0.6% among the entire population. Similar results were obtained in the Los Angeles education system, where 0.8% of students and staff tested positive. A statement in the local press of the antigen pharmaceutical company claimed a false-positive rate of only 0.6%. Indeed a small number but currently identical to the COVID-19 distribution in the entire population. The immediate result: The number of correct positive diagnoses will be about the same as the number of false alarms, meaning around only a 50% chance that you are infected given a positive answer.
It is important to clarify that the decision of having a large antigen examination of the students’ population was made among experts, and may be the least bad alternative. But it means identifying a large number of healthy people as infected and putting them in isolation. Again, probably still a desirable option over non-identifications of a large number of truly infected people.
“Well, the way of paradoxes is the way of truth. To test Reality we must see it on the tightrope. When the verities become acrobats, we can judge them.”
– Oscar Wilde, The Picture of Dorian Gray
Applying what we have learned to cyber threat detection systems
Can I trust any cyber threat detection system?
Cyberattacks could be a very rare event compared to the entire population or quite common, depending on the specific domain and the phenomena to be identified. For example, data breaches are quite rare compared to all database transactions while web application attacks can be very common. That means that the higher the FPR rate and the lower probability for the security phenomena, the system will generate a higher number of false alarms relative to the number of true attack cases.
Studies show that many organizations suffer from alert fatigue where most events are defined as false alarms. Moreover, another survey shows that 66% of the organizations had doubts about security systems and disregard alarms as a result of previous FP incidents. Just imagine the overload (and frustration) this figure has on corporate SOC teams.
The Imperva approach
One of the burning questions when dealing with FP in the cyber domain is the very delicate balance between missing out on a real attack (FN) and the overloading of false alarms (FP) and thus impairing the reliability of the product over time and its effectiveness. There is no one answer and each case is unique. It very much depends on the use case at hand, but there are a set of tools that we frequently use in our research and development process. This approach is also valid as a general scheme for any other domain.
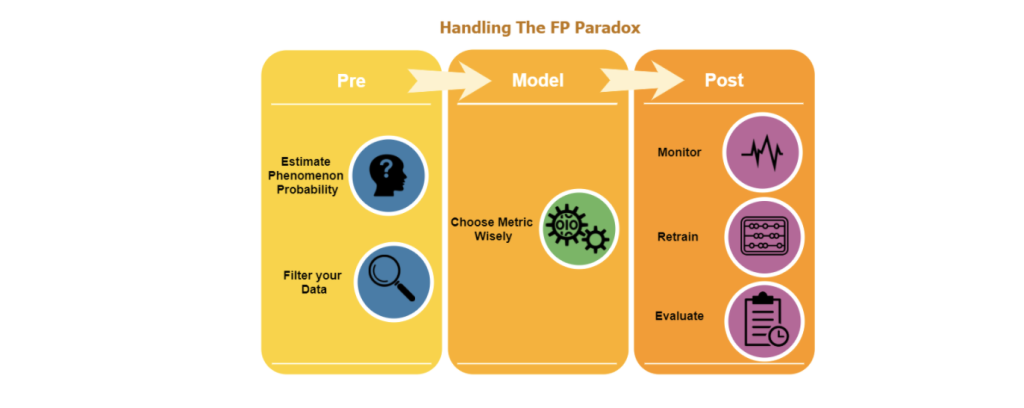
Figure 2: Set of tools for handling the FP paradox
Let’s say we want to build a classifier that identifies HTTP requests originating from bad bots towards our website.
Pre
To be on the safe side of Equation 1, we have to assess the rarity of the phenomenon we’re trying to find. In this case, web application attacks executed by bad bots. Based on Imperva’s annual report, bad bot traffic is responsible for 25% of all traffic to all websites. Another way to further analyze the phenomena rarity is to categorize the website to a particular industry (link, page 18). For example, if my website is a financial services provider, we can estimate the bad bots traffic activity to 18.9%.
In addition, we have seen the risk of running tests on large populations and therefore we will have to filter the data based on preliminary information. Reducing and targeting the population can help us increase the probability of this phenomenon. In the medical domain, this was done by a list of symptoms, proximity to a verified patient, or the medical history. In our case, the equivalent will be, for instance, the history of the IP (our patient) or the device. We can use tools like IP reputation to examine a previous user’s activity and filter only IPs with suspicious or abnormal behavior, such as access from an unseen country or to a new resource.
Model
While training the model and choosing its hyperparameters, it is important to note the metric you wish to optimize: are you more concerned with FP or FN. You can use one of the existing metrics or predefined your metric (for example, a FP result will be 5 times worse than an attack that was missed).
Post
It’s important to monitor your model in production and re-train it to reduce FP. Cyberattacks are dynamic, so you have to keep your eyes open and keep your model as up-to-date as possible. You can think of it as the equivalent for early detection of new COVID-19 variants. Another important approach is validating the results obtained with an expert. In the medical world, you will probably consult with a doctor. Here the second look of a cybersecurity specialist may be useful. Another option could be to mechanize this process by using another FP detection model that accepts the context of the attack.
Some takeaways
FP is a challenge. What can you do about it?
Realize that small FP rates can still be a very big issue. There is no perfect system and mistakes cannot be avoided. But once we understand how every fraction of a percent improvement in metrics like FP can be significant, we know that accuracy is not all and that we need to keep the FP measure as small as possible.
Stay focused
The rule of thumb for the FP paradox says it is not possible to diagnose a phenomenon whose probability is lower than the FP of the detection process. Therefore running these tests on a large scale or random samples could be disastrous. Pre-processing and filtering should be performed. Instead of running on all your data, first try to pre-identify and run only on the suspicious part, data that we have reason to believe represent the phenomena.
Expertise
Finally, you cannot rely only on machines or any statistical systems and often need an expert opinion. Just as in the world of medicine, where there is no replacement for a doctor’s opinion, so too in the cybersecurity world a deep understanding of an analyst or researcher is required. Domain knowledge is the key.
Acknowledge
“How wonderful that we have met with a paradox. Now we have some hope of making progress.” – Niels Bohr
Even if the above sounds perhaps trivial it is half the way to a solution. Dealing with a problem is first acknowledging that you have a problem and knowing its sources.
Once the phenomenon is recognized, we can see that machine learning or any other statistical system, however accurate it may be, should be operated with caution and under the appropriate conditions, taking into account the probability of the phenomenon we are trying to find and the data we are working with.
Try Imperva for Free
Protect your business for 30 days on Imperva.